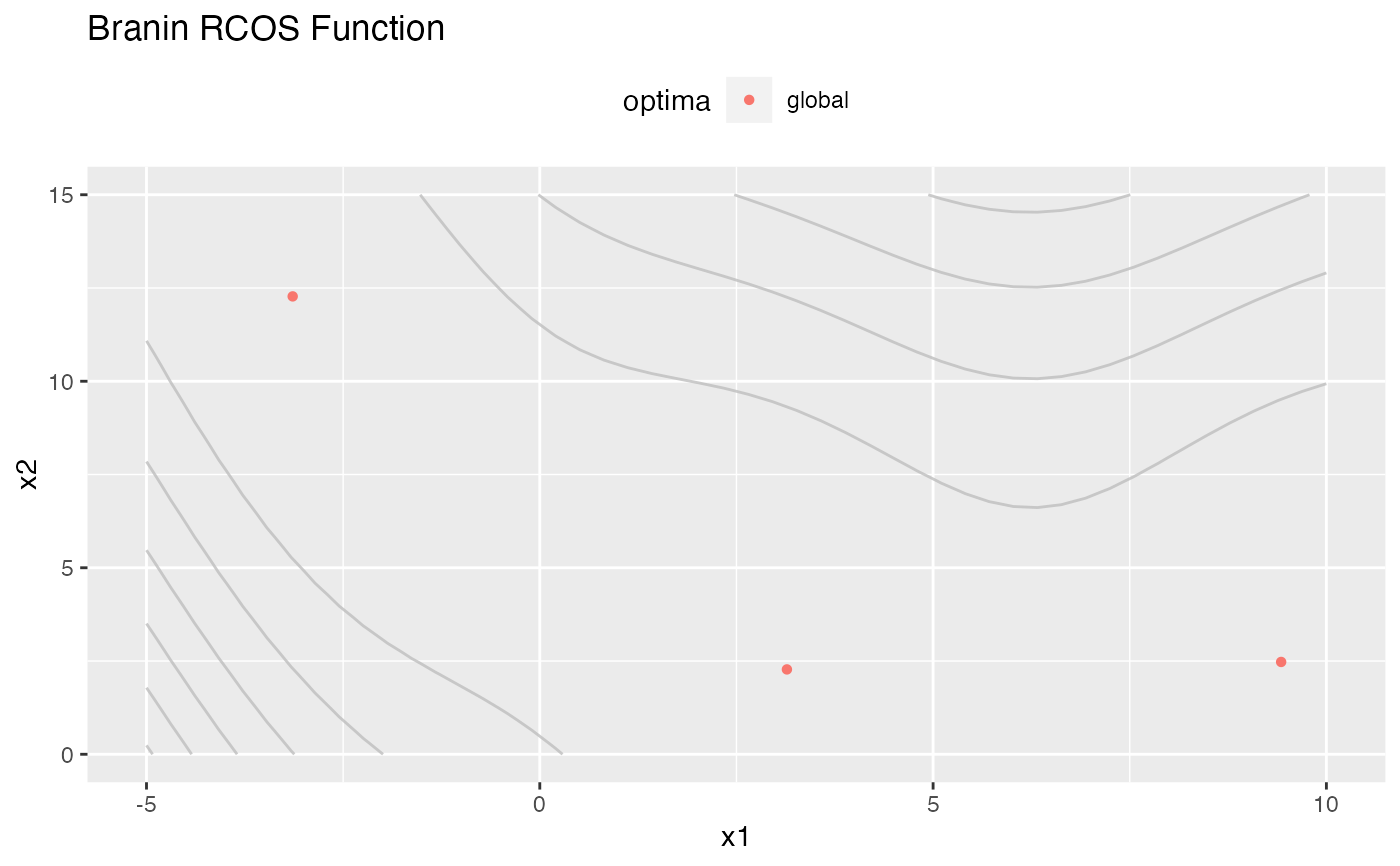
Popular 2-dimensional single-objective test function based on the formula: $$f(\mathbf{x}) = a \left(\mathbf{x}_2 - b \mathbf{x}_1^2 + c \mathbf{x_1} - d\right)^2 + e\left(1 - f\right)\cos(\mathbf{x}_1) + e,$$ where \(a = 1, b = \frac{5.1}{4\pi^2}, c = \frac{5}{\pi}, d = 6, e = 10\) and \(f = \frac{1}{8\pi}\). The box constraints are given by \(\mathbf{x}_1 \in [-5, 10]\) and \(\mathbf{x}_2 \in [0, 15]\). The function has three global minima.
makeBraninFunction()Value
[smoof_single_objective_function]
References
F. H. Branin. Widely convergent method for finding multiple solutions of simultaneous nonlinear equations. IBM J. Res. Dev. 16, 504-522, 1972.
Examples
library(ggplot2)
fn = makeBraninFunction()
print(fn)
#> Single-objective function
#> Name: Branin RCOS Function
#> Description: no description
#> Tags: single-objective, continuous, differentiable, non-separable, non-scalable, multimodal
#> Noisy: FALSE
#> Minimize: TRUE
#> Constraints: TRUE
#> Number of parameters: 2
#> Type len Def Constr Req Tunable Trafo
#> x numericvector 2 - -5,0 to 10,15 - TRUE -
#> Global optimum objective value of 0.3979 at
#> x1 x2
#> 1 -3.141593 12.275
#> 2 3.141593 2.275
#> 3 9.424778 2.475
print(autoplot(fn, show.optimum = TRUE))